Quando uma corda vibra, perde energia gradualmente. No mundo quântico, explicar este fenómeno foi uma tarefa difícil durante mais de um século. Agora, um estudante conseguiu encontrar a solução exata, o que abre novas possibilidades.
No início do século XX, o físico britânico Horace Lamb propôs um modelo para descrever o comportamento de uma partícula vibrante num meio elástico. Este problema era bem conhecido na física clássica: quando vibra, uma partícula gera ondas que se propagam pelo meio e, por sua vez, dissipam a energia do sistema. No entanto, quando surgiu a necessidade de traduzir esse fenómeno para a linguagem da mecânica quântica, surgiram obstáculos que se prolongaram… até hoje. Um século depois, um estudante universitário e o seu mentor conseguiram resolver este enigma no contexto da física quântica. A área dos osciladores quânticos está repleta de possibilidades futuras.
Nam H. Din, juntamente com o seu professor Dennis P. Claugherty, encontrou a solução exata para o chamado modelo quântico de Lamb, que descreve o comportamento de um oscilador harmónico amortecido à escala atómica. A descoberta, publicada na revista Physical Review Research, resolveu um problema colocado em 1900, com a ajuda de ferramentas modernas da mecânica quântica. O mais impressionante é que um dos autores ainda era um estudante de mestrado quando apresentou o seu trabalho. A sua contribuição foi decisiva para resolver o modelo, que até agora resistia a todas as tentativas de encontrar uma solução rigorosa na mecânica quântica.
Do modelo clássico ao quântico
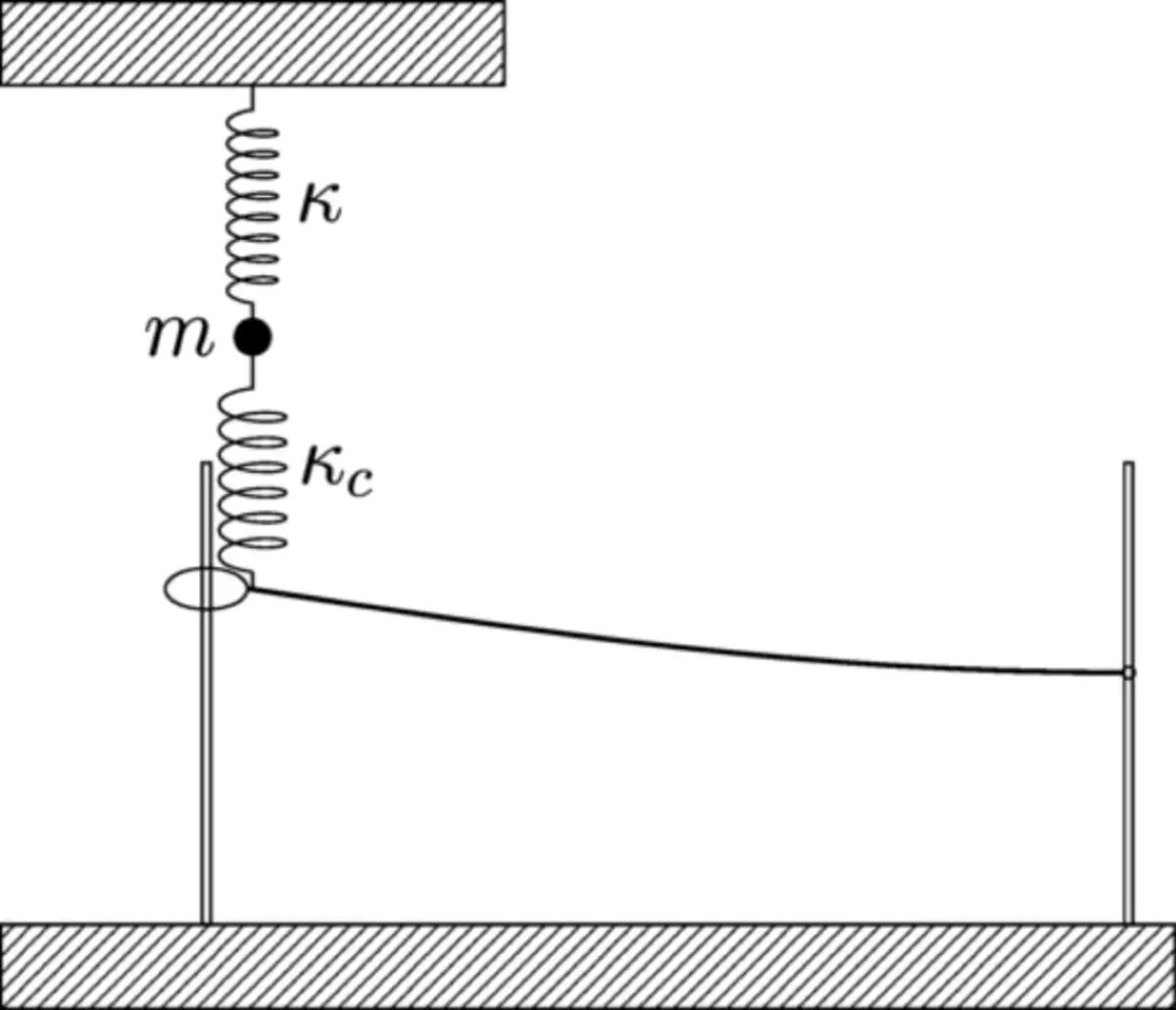
O modelo original proposto por Lamb descrevia como uma partícula vibrante perde energia, gerando ondas num meio contínuo. Essa perda de energia — o amortecimento — podia ser explicada pelas leis de Newton e era considerada resolvida no quadro clássico. Mas quando os físicos tentaram transferir essa mesma ideia para o mundo dos átomos, surgiram contradições fundamentais com os princípios da mecânica quântica.
Um dos maiores problemas era conciliar o comportamento dissipativo do sistema com o princípio da incerteza de Heisenberg, que impõe restrições rigorosas à precisão com que é possível determinar simultaneamente a posição e o momento de movimento de uma partícula. Incorporar a perda de energia num sistema quântico sem violar este princípio foi, durante décadas, um obstáculo intransponível.
Ding e Claugherty reformularam o modelo de Lamb, adaptando-o ao contexto quântico, mas sem simplificações que lhe tirassem a riqueza física. A sua proposta mantém a estrutura original do sistema, dividido numa partícula vibratória (oscilador) e num meio que atua como ambiente (corda), mas inclui formalmente a ligação entre estes dois elementos sob a forma de operadores bilineares. Esta formulação permitiu aplicar uma transformação matemática conhecida como transformação de Bogoliubov, com a qual foi possível resolver o sistema com precisão.
Solução exata após 125 anos

A principal conquista deste trabalho é encontrar uma solução exata para um sistema físico que até agora só podia ser descrito de forma aproximada. O artigo enfatiza que «o modelo fornece um exemplo solucionável de um oscilador harmónico quântico amortecido». Isso significa que não se trata de uma simulação ou solução parcial. Ou seja, o sistema foi descrito matematicamente em toda a sua complexidade, respeitando as regras da mecânica quântica.
Além disso, os autores calcularam a frequência de oscilação do sistema e o coeficiente de amortecimento usando uma equação integral não linear, o que lhes permitiu também descrever o estado básico do sistema. Este estado, que está longe de ser simples, representa um vácuo multimodal comprimido, uma configuração quântica na qual a incerteza da posição da partícula diminui com o aumento da incerteza do momento.
Esta ideia de redistribuição da incerteza já tinha sido utilizada anteriormente na física para aumentar a precisão das medições, por exemplo, em detetores de ondas gravitacionais. Mas agora, graças ao trabalho de Clougherty e Dinh, foi provado que tais estados podem surgir naturalmente em sistemas físicos específicos.
De acordo com o artigo, o estado básico obtido «é sempre um estado de vácuo multimodal comprimido», o que confirma que a natureza quântica do sistema se reflete mesmo na sua configuração mais estável. Partindo disso, os investigadores também calcularam o espectro de excitações e a forma de propagação da energia pelo sistema.
Estado de vácuo comprimido multimodal: um estado quântico incomum, mas fundamental
O chamado estado de vácuo comprimido multimodal é o estado básico do sistema descrito por Clougherty e Dinh. É uma forma especial de vácuo quântico — um estado com a menor energia possível — ao qual foi aplicado um processo matemático chamado compressão quântica (squeezing). Isso permite reduzir a incerteza em uma propriedade específica do sistema (por exemplo, na posição), aumentando a incerteza em outra (por exemplo, no momento), sempre respeitando o princípio da incerteza de Heisenberg. A novidade reside no facto de que essa compressão não ocorre em um único modo de oscilação, mas simultaneamente em muitos modos diferentes do sistema, o que lhe confere um caráter «multimodal».
Este tipo de estado já era conhecido na ótica quântica e na teoria quântica de campos, mas o seu aparecimento como solução precisa e natural num sistema físico específico, como neste modelo, não é um fenómeno comum. O estado de vácuo comprimido multimodal reflete com precisão a interação entre uma partícula oscilante e o seu ambiente e permite calcular propriedades importantes, como a velocidade de dissipação ou a distribuição de excitações. Este estado não é uma construção abstrata, mas tem aplicações práticas em áreas que exigem medições extremamente precisas, como detectores de ondas gravitacionais ou tecnologias de sensores quânticos.
O papel fundamental do jovem investigador

Nam H. Dinh era estudante de mestrado quando contribuiu para esta descoberta.
Depois de obter o mestrado em Física pela Universidade de Vermont em 2024, trabalhou com Claugherty neste modelo durante o doutoramento e atualmente está a trabalhar na sua tese de doutorado em Matemática. O seu papel foi longe de ser secundário: a sua participação permitiu derivar e resolver equações que outros autores evitaram devido à sua complexidade.
A colaboração entre os dois autores permitiu aproveitar tanto a experiência de Claugherty quanto a versatilidade matemática de Nam. Este trabalho não é apenas uma demonstração técnica, mas um exemplo de como o talento jovem pode realmente influenciar a investigação fundamental. Em vez de simplificar o sistema ou recorrer a métodos puramente numéricos, eles conseguiram manter a estrutura analítica do modelo até ao fim.
«Na física clássica, sabe-se que quando os objetos vibram ou oscilam, eles perdem energia devido ao atrito, resistência do ar, etc.», diz Din. «Mas no modo quântico isso não é tão óbvio», acrescenta ele.
Significado prático e aplicações futuras
Embora o trabalho seja de natureza teórica, as suas implicações práticas são evidentes. Uma delas é a possibilidade de desenvolver sensores quânticos mais precisos, capazes de medir distâncias ou mudanças extremamente pequenas. Isto deve-se ao facto de que, à medida que a incerteza da posição diminui, é possível realizar medições abaixo do limite quântico padrão.
O modelo prevê como a incerteza muda dependendo da ligação entre a partícula e o ambiente e permite calcular com precisão a velocidade de dissipação de energia. Esta informação pode ser útil para compreender sistemas reais, tais como átomos em corpos sólidos, oscilações em nanoestruturas ou esquemas quânticos que devem minimizar a perda de coerência.
Isso também abre possibilidades para o estudo de outros sistemas físicos com estrutura semelhante. Os autores observam que os seus resultados podem ser aplicados a «uma série de sistemas quânticos relacionados», como modos de oscilação em isolantes magnéticos ou cavidades eletromagnéticas. Isso torna o modelo quântico de Lamba uma ferramenta de referência para a investigação de novas configurações físicas.
Esta conquista não é apenas uma vitória da física teórica, mas também uma possível fonte de inspiração para o desenvolvimento de experiências que testarão essas previsões. A precisão alcançada pelo modelo permite comparar os seus resultados com dados experimentais em plataformas como sistemas optomecânicos ou ressonadores quânticos.




























